资料查阅
硕士(2篇)
| 题名 | 作者 | 学校 | 年份 | 备注 |
|---|---|---|---|---|
| 基于OpenCV的机器人双目手眼标定系统的研究与实现 | 李明超(控制) | 山东科技 | 2012 | OpenCV2.2;适合入门;流程详细:相机标定、立体标定、手眼标定 |
| 工业机器人手眼标定技术研究 | 张云珠(检测) | 哈工程 | 2009 |
期刊(3篇)
| 题名 | 期刊 | 学校 | 年份 | 备注 |
|---|---|---|---|---|
| 基于双目视觉的六自由度工业机器人控制系统研究 | 工业仪表与自动化装置(中文核心) | 陕西工业职业技术学院 | 2017 | MATLAB标定相机内外参数、OpenCV抓取特征;泛泛介绍,没啥用 |
| 大视场双目立体视觉柔性标定 | 光学精密工程(Ei) | 西北工业大学 | 2017 | 使用编码标志点作为标定板;测量空间1200×1000×1000,测量精度优于0.1,单位mm |
| 基于OpenCV的码垛机器人手眼标定方法 | 制造技术与机床 | 广东工业大学 | 2018 | 单目;OpenCV;精度±1mm;缺陷:只有x,y,没有z和姿态信息 |
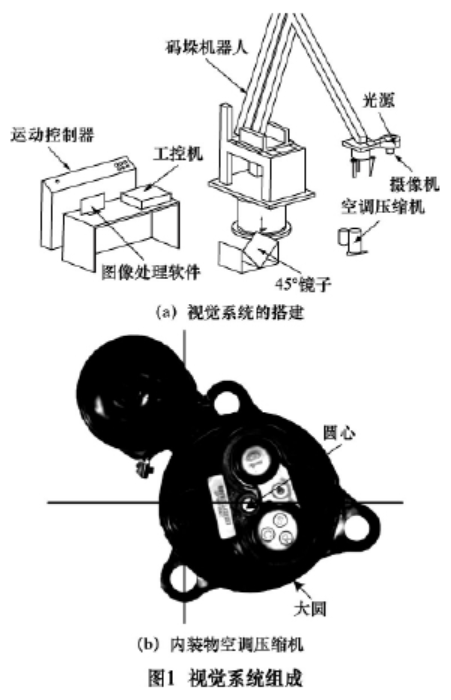
期刊_基于OpenCV的码垛机器人手眼标定方法
单目
Eye-in-Hand式手眼系统:摄像机固联于机械手的末端
重点公式
式(6):图像坐标系=>世界坐标系
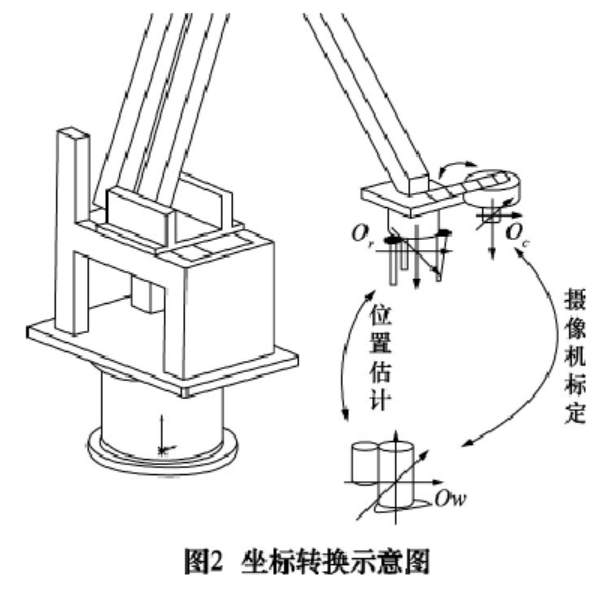
手眼标定:基于OpenCV的“两步”标定法
图像坐标系 ↔ 机械手坐标系
(空调压缩机图像坐标系下的坐标值对应的机械手坐标系的坐标值)
相机标定:采用张正友标定法,以棋盘格图像作为标定的参照物
世界坐标系 ↔ 图像坐标系
空调压缩机大圆圆心坐标为(X,Y,Z),某姿态下的棋盘图像与空调压缩机所在平面共面
故该状态下棋盘的外参数=空调压缩机世界坐标与图像坐标转换的外参数
故由式(1)可求得图像坐标(x,y,z)对应的世界坐标(X,Y,Z),完成摄像机标定(OpenCV采用的是介于传统标定法与自标定法之间的非线性模型摄像机标定法)
式(1):
- 为摄像机内参数
- 为外参数
- 为尺度因子
“四点”位姿估计:在机械手坐标系上设定四个标记点(内装物所在平面)进行位姿估计
世界坐标系 ↔ 机械手坐标系
由于视觉定位是为了使空调压缩机大圆圆心与图像中心重合。当手爪没有达到这个位置时,视觉系统必须知道圆心相对于图像中心的位置,即机器人需要移动的距离,如式(6)。
在机械手处于原点状态下,将标记点依次置于机械手坐标系中,实现世界坐标系与机械手坐标系的转换。
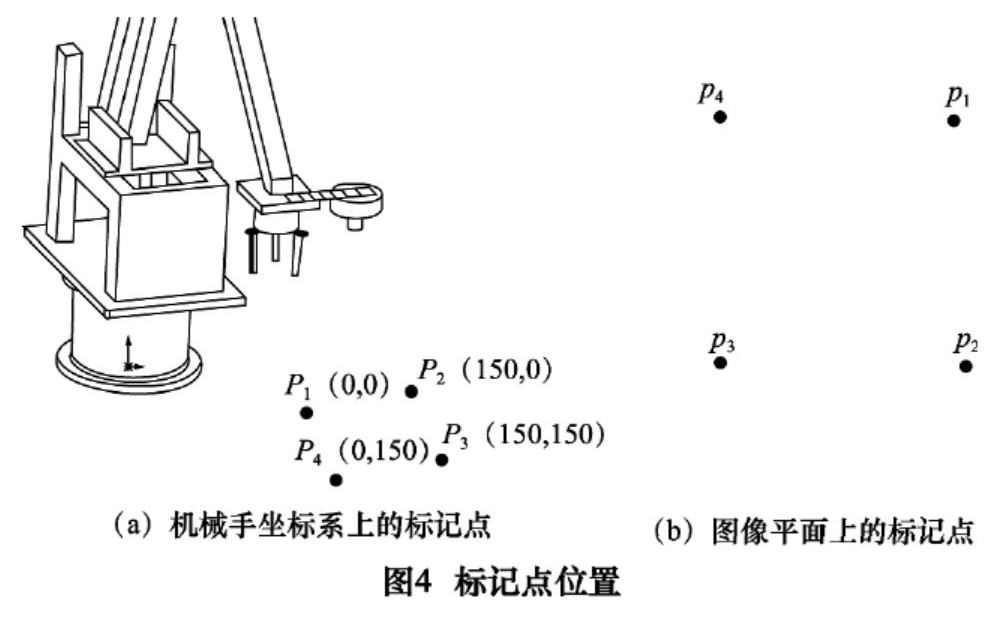
机械手坐标系中的标记点P1~P4与相机图像平面上的点p1~p4的变换由旋转向量(rvec)和平移向量(tvec)来定义 => 欧式变换/刚性变换,具体形式为式(2)
式(2):
由于空调压缩机都放置于同一平面上,故令圆心坐标Z=0
一个平面到另一个平面的投影映射,又称两幅图像之间的单应性H,具体形式为式(3),也即式(4)
PS:式(3)貌似有问题
式(3):
式(4):
- x、y为空调压缩机图像坐标值
- X、Y为空调压缩机机械手坐标值
令
可得:
式(5):
故:
式(6):
也即机器人要移动的坐标值。
OpenCV API
| 模块 | 功能 | 3.4.1中的py函数 |
|---|---|---|
| 相机标定 | 对棋盘格标定 | cv2.calibrateCamera() |
| 位姿估计 | 输入:图像坐标值、机械手坐标值、摄像机内参数、畸变系数。输出:旋转向量、平移向量 | cv2.solvePnP() |
| 位姿估计 | 输入:旋转向量、平移向量。输出:旋转矩阵、平移矩阵 | cv2.Rodrigues() |
| 位姿估计 | 输入:标记点的世界坐标值、旋转矩阵、平移矩阵。输出:投影得到的图像标记点的二维坐标值 | cv2.projectPoints() |
| 位姿估计 | 输入:投影得到的图像标记点的二维坐标值、实际上的图像标记点的坐标值。输出:投影误差 | cv2.norm() |
论文缺陷
只有x,y,没有z(Z=0)和姿态信息,相机标定时所有棋盘格均处于同一平面上
自己设定4个点,故知道机器人处于原点时,4个点在机械手坐标系下的坐标值
相当于极大简化后的流程
硕士_基于OpenCV的机器人双目手眼标定系统的研究与实现
重点公式
(式3.32)、(式4.7)、求解思路
扫盲
- 机器视觉的主要目标:三维重建、空间定位、图像处理、模式识别、运动分析
- 机器人视觉系统:固定式、手眼式
- 双目手眼视觉定位系统 = 机器人手臂(手)上加上双目摄像机(眼)
思路:利用双目相机获得空间目标位置 → 通过手眼关系转换到机器人坐标系下 → 得到目标在机器人坐标系下的坐标 - 目标立体定位 = 一系列的标定过程 = 物体相对于机器人坐标系的坐标 → 机器人手爪移动到目标的位置
思路:
①通过单相机标定求得双目摄像机中的一个摄像机相对于目标物体的位置关系 → 通过立体标定求得左右摄像机的位置关系 → 得到两个摄像机相对于目标的关系
②通过手眼标定求得摄像机固定在手爪上时的确定的位置关系
③ → 间接的通过摄像机相对于目标的关系和手眼关系确定机器人手爪相对于目标物体的关系
摘要
- 本文研究:立体标定、手眼标定
- 双目手眼标定系统 = 立体标定(=单目相机标定 + 双目相机之间的关系标定) + 手眼标定
- 单目相机的非线性模型的标定:Zhang和Heikkila相结合的标定方法
- 双目相机之间的相对位置关系:通过优化方法
- 手眼标定:Tsai方法
- 立体标定需要9个位置的棋盘格图像,手眼标定需要3个位置的目标图像
- 双目手眼视觉定位系统整体流程:
- 把双目摄像机装在机器人末端执行器上
- 当末端执行器运动时,摄像机跟随其运动,摄像头对目标物体进行取像
- 然后传输到计算机中,通过编程进行参数计算
- 最终实现目标的准确定位
- 双目手眼视觉定位系统标定流程:
- 对摄像机进行标定,得到摄像机内参数和畸变系数
- 利用得到的摄像机参数进行手眼系统标定,得到手眼关系矩阵
- 软件:VS2018、C++、OpenCV
- 硬件:MOTOMAN-SV3X
实验环境
硬件
- MOTOMAN工业机器人
- POINT GREY Bumblebee2双目摄像机
- 1394图像采集卡
- 机器人控制柜
- 黑白棋盘格标定板
- 标定板支架
- 研华工控机
| 设备 | 型号 | 备注 |
|---|---|---|
| 工业机器人 | 日本安川的MOTOMAN-SV3X | 6自由度,重复定位误差<±0.03mm,包含6部分:机器人本体、YANSNAC XRC控制柜、供电电缆、气动手抓器、变压器、YASNAC XRC示教编程器 |
| 标定摄像机 | 加拿大POINT GREY的Bumblebee2多视点视频立体相机 | 实时3D数据转换、相机位置偏差和镜头畸变自动校正、方便应用与集成、具有高质量的CCD传感器和高速1394接口 |
| 图像采集卡 | 1394图像采集卡 | |
| 计算机 | 研华IPC-610MB-L工控机 | Intel Core(TM) 2 Duo CPU E7500 2.93GHz;2,99GDDR 内存;采用Windows XP操作系统 |
| 标定板和支架 | 黑白棋盘格标定板 | 方格的个数是12×11,每个方格大小为30mm×30mm |


软件
- VS2008
- OpenCV 2.2:图像处理模块、相机标定模块
相机标定原理
三维重建:从物体的二维图像出发恢复出空间点三维坐标的过程
三维重建的3个关键步骤:
- 图像对应点的确定
- 相机标定
- 两图像间摄像机运动参数的确定
图像坐标系、摄像机坐标系、世界坐标系
图像坐标系中的像素单位、物理单位
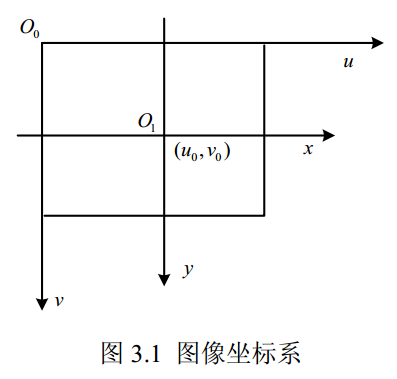
- 以像素为单位的直角坐标系(u,v)——像素单位
- ,为每一个像素在x轴、y轴上的物理尺寸
- 以毫米为单位的物理直角坐标系(x,y)——物理单位
- 是x,y坐标系的原点,一般位于图像的中心点,是摄像机光轴与图像平面的交点
图像中某一点在这两个坐标系下的关系(式3.1):
矩阵形式:
像素单位 ← 物理单位(式3.2)
物理单位 ← 像素单位(式3.3)
世界坐标系与摄像机坐标系
- 摄像机坐标系(空间三维,,)
- 轴是摄像机的光轴,垂直于图像坐标系
- 是摄像机的光心
- 摄像机焦距f是光心与图像坐标系中点的连线
- 世界坐标系(空间三维,,)
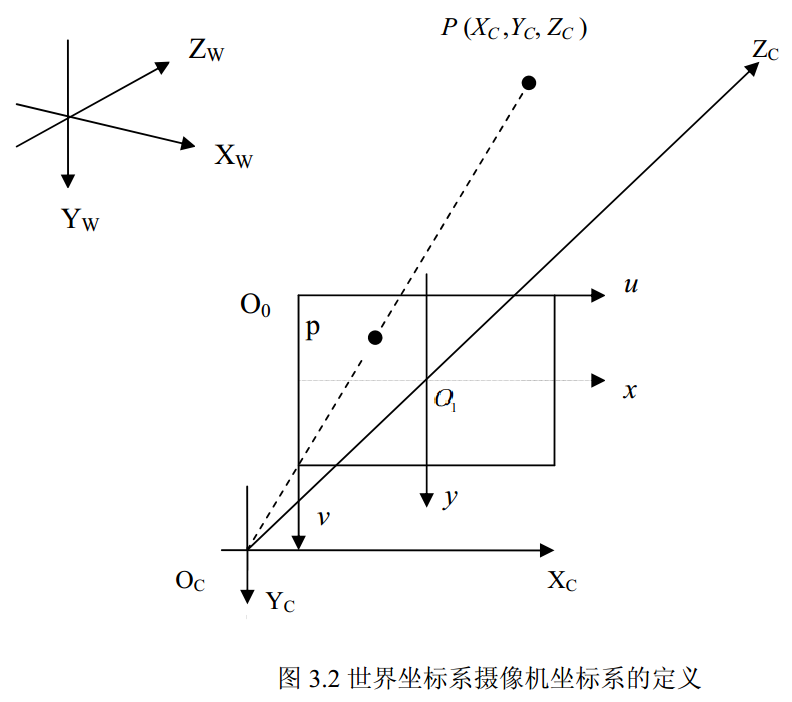
矩阵形式:
空间某一点P:
- 在摄像机坐标系的齐次坐标
- 在世界坐标系的齐次坐标
- 两个坐标系之间的位置关系:旋转矩阵R、平移向量t
- 旋转矩阵R是3*3的正交单位矩阵
- 平移向量t是三维列向量:
- 摄像机坐标系与世界坐标系的关系(式3.4)
线性摄像机成像模型(针孔模型)
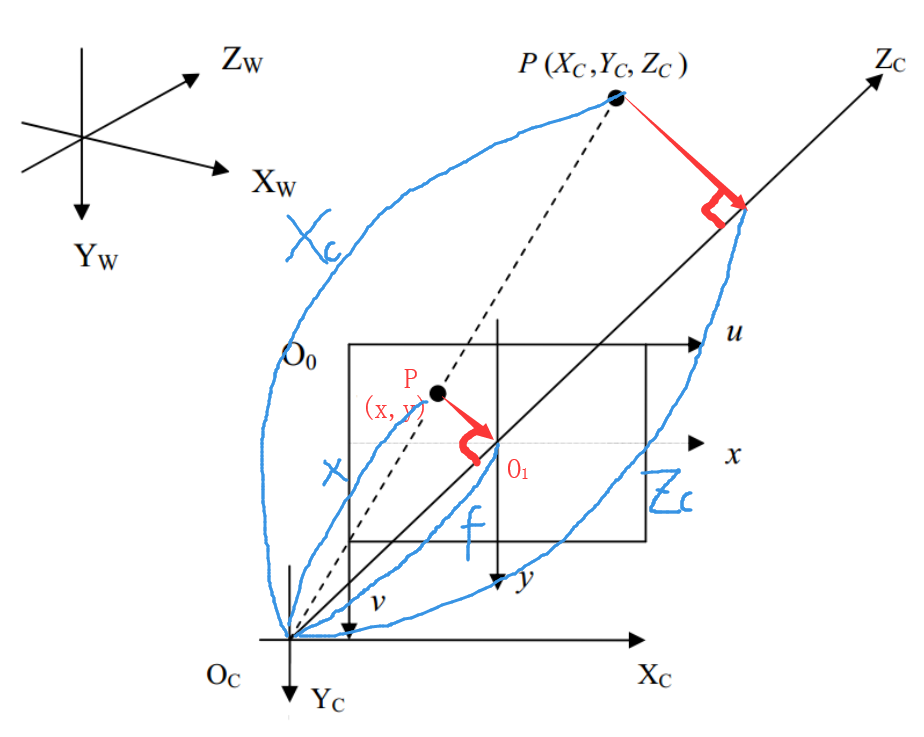
- 为空间中任一点点与摄像机光心的连线与图像平面的交点
- f为摄像机焦距
- 三角几何关系(式3.5):
矩阵形式(某一点在摄像机坐标系和以毫米为单位的图像坐标系之间的关系)(式3.6):
(式3.6)+(式3.3)=P点摄像机坐标与像素坐标之间的关系=(式3.7):
整理可得(式3.8):
(式3.8)+(式3.4)=P点在世界坐标系与图像坐标系下的关系=(式3.9):
其中,
小结,某一点P从图像坐标系转换到世界坐标系仅需两个变换矩阵:
- 为摄像机的内参数矩阵:只与摄像机内部结构有关
- 为摄像机的外参数矩阵:完全由摄像机相对于世界坐标系的方位决定
所谓的相机标定就是求解这个两个参数矩阵
各坐标系之间的关系
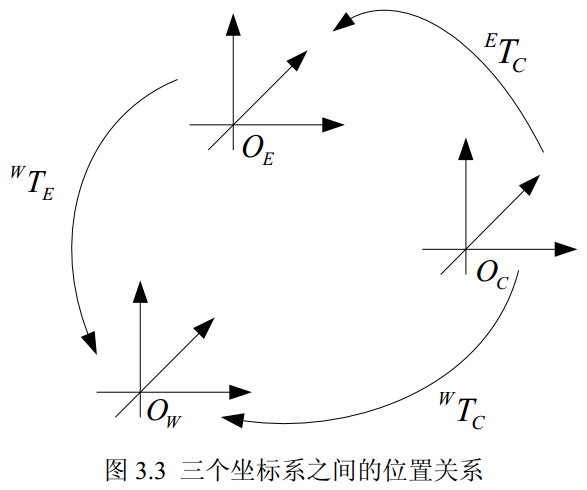
- 世界坐标系:机器人基座所在的坐标系
- 摄像机坐标系
- 机器人手爪坐标系
- 转换关系: →
- 转换关系: →
- 转换关系: →
- 为机器人手爪坐标到机器人基坐标(=世界坐标系)的旋转映射矩阵,大小为3×3,由机器人手爪的姿态决定,与机器人手爪所在位置无关
- 为机器人手爪坐标到机器人基坐标的平移向量
- .
- 为摄像机坐标到机器人手爪坐标的旋转映射矩阵
- 为摄像机坐标到机器人手爪坐标的平移向量.
(式3.10):
设P为空间一点,、、分别为P点在、、下的坐标值
其中、齐次坐标分别为、,则有:
(式3.11):
(式3.10)+(式3.11)=(式3.13):
整理,得(式3.14):
由(式3.8),得(式3.15):
T是一个3×3的摄像机内部参数矩阵,是一个可逆矩阵,有(式3.16):
(式3.14)+(式3.16)=(式3.17):
式中:
- 、是机器人手爪相对机器人基坐标的旋转矩阵、平移向量,可直接从机器人控制器中读取
- 、是摄像机相对机器人手爪坐标的旋转矩阵、平移向量,在手眼系统中是固定不变的
- T是一个3×3的摄像机内部参数矩阵,可通过相机标定求出,是固定不变的
- (u,v)通过对图像处理计算可以得到
- 故问题的关键在于求:、
非线性摄像机成像模型
相机标定可以修正图像畸变
3种图像畸变:
- 径向畸变
- 离心畸变、薄透镜畸变:包含径向畸变、切向畸变
式中:
- 为实际得到的图像点的坐标
- 为理想的针孔型模型计算出的图像点的坐标
- 为非线性模型中的畸变值,是各种畸变的总的表示,大小与图像点在图像中的位置有关
式中:
- 第1项为径向畸变
- 第2项、第3项为离心畸变、薄棱镜畸变,可忽略
- 非线性畸变参数:
只考虑径向畸变,
其中,
x方向与y方向的畸变相对值()与径向畸变成正比,故图像边缘发生的畸变较大
只考虑径向畸变的非线性模型中的内参数矩阵:
其中,γ是图像上两个轴的扭曲参数
立体标定
在立体视觉系统中,一般用两台摄像机
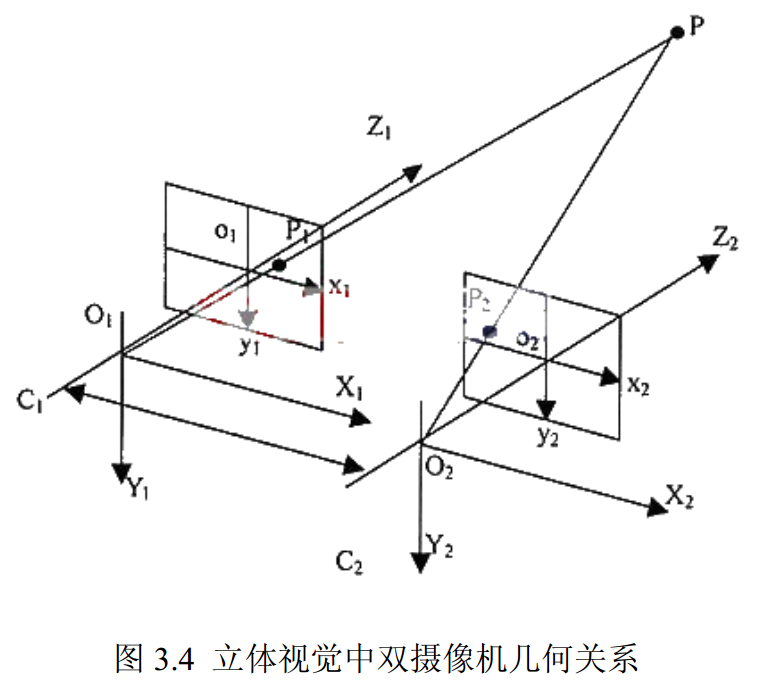
立体标定的目的:标定两台摄像机之间的几何关系
立体标定的过程:对左右两台摄像机分别进行相机标定,得到两台摄像机的内参数矩阵、外参数矩阵(旋转矩阵、平移向量,表示为)
外参数的物理意义:摄像机相对于世界坐标系的关系
设某一点P在世界坐标系和两个摄像机坐标系下的非齐次坐标为
消去:
故,两个摄像机之间的几何关系用R和t表示:
故,若知道每一个摄像机的外参数矩阵,则两台摄像机之间的几何关系可以通过计算得出
立体视觉定位系统
原理:用两台摄像机同时观察目标物体并获取图像,由于两台摄像机位置不同,在获得的图像中存在视差。利用视差原理,根据三角关系就可以确定该物体的深度信息,包括目标物体的空间位置坐标。从而实现对目标物体的抓取。
思想:根据已知的图像坐标(通过图像处理得到),求取目标的空间坐标。
立体定位的求解过程:
由(式3.16)摄像机坐标系与图像坐标系之间的关系,左、右摄像机有关系式:
(式3.25):
(式3.26):
由(式3.14)摄像机坐标系与世界坐标系之间的关系,左摄像机有关系式(式3.27):
(式3.25)+(式3.27)=(式3.28)左图像坐标系与世界坐标系之间的关系:
立体标定中得到的左右摄像机关系矩阵(式3.29):
(式3.27)+(式3.29)=(式3.30)右摄像机坐标系与世界坐标系之间的关系:
(式3.26)+(式3.30)=(式3.31)右图像坐标系与世界坐标系之间的关系:
(式3.28)+(式3.31)=(式3.32)空间某一物体P在左右图像坐标系与世界坐标系之间的关系:
式中:
- 为目标物体P在左右图像坐标系中的像素坐标,可通过图像处理得到
- 为机器人手爪坐标到机器人基坐标的旋转映射矩阵、平移向量,可通过机器人控制读取
- 为左摄像机坐标相对于机器人手爪坐标的旋转矩阵、平移向量,可通过手眼标定得到
- 是右摄像机坐标相对于左摄像机坐标之间的旋转矩阵、平移向量,可通过摄像机的立体标定得到
- 为未知参数
- 为目标物体P在世界坐标系的坐标值,是3×1的列向量,是要求的变量
- 为左右摄像机内部参数矩阵,可通过相机标定得到
- 故把求得的代入(式3.32),得到6个方程,未知数为5个,故方程有唯一解
- 故,输入,输出,实现图像坐标系到机器人基坐标的映射,是目标立体定位的思想
手眼标定原理
输入:左摄像机的内参数、其拍摄的图像、不同位置的机器人姿态坐标参数
输出:手眼关系矩阵
手眼标定的参数
- :空间某一个物体所在的坐标系
- :摄像机坐标系
- :机器人手爪坐标系
- 与的相对位置已知,可通过相机标定求得(旋转矩阵)、(平移向量)
- 若再有、的相对位置,可求、的相对位置
- 手眼标定关键:求解R和t的过程(双目摄像机安装在机器人手臂上,、之间的相对位置是固定的,为R和t)
求解机器人手眼标定问题的基本思路:
使摄像机从空间不同的方位对已知目标进行取像,并记录这些位置的机器人姿态参数,利用这些图像信息和机器人姿态参数推导出关于R和t的多个关系方程组,用最小二乘法求解之。
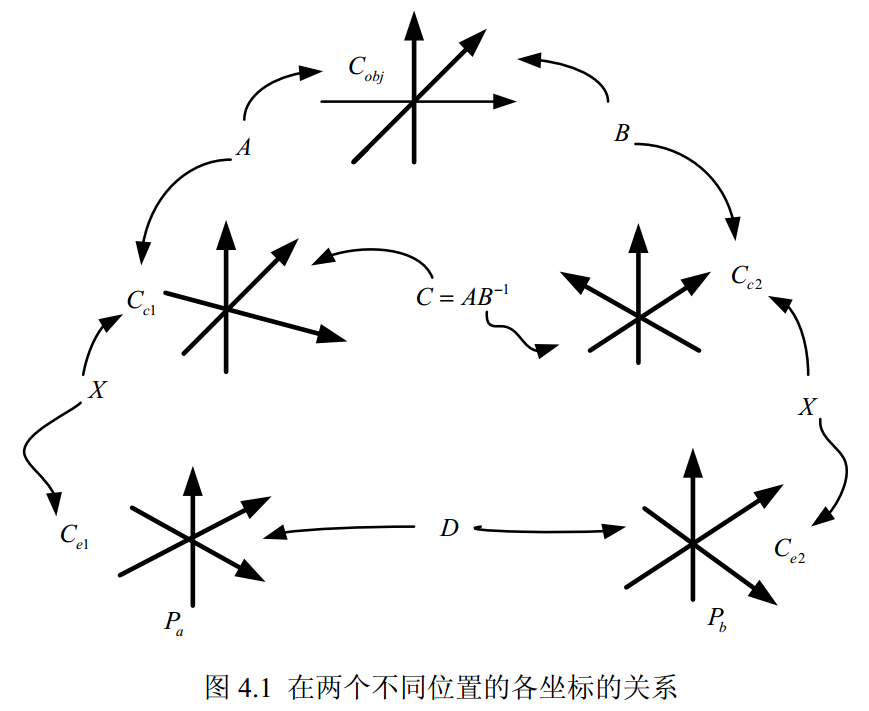
两个坐标系之间的关系用四阶方阵(A,B,C,D,X)表示,包含旋转矩阵、平移向量(下标表示矩阵名称):
图4.1中:
- 、:平台运动前的摄像机坐标系、机器人坐标系
- :标定参照物的坐标系=前文中的世界坐标系
- 、:平台运动后的摄像机坐标系、机器人坐标系
- 、:在这两个位置上进行相机标定求得的外参数(、与的相对方位)
- :摄像机从运动到这两个位置之间的关系,有(A、B已知,故C为已知矩阵)
- :机器人手爪在这两个位置的相对关系,可通过已知数据(机器人手爪的位置坐标可通过机器人控制器直接读取)计算求得
- :机器人的手眼关系,固定值,求解X的过程就是机器人的手眼标定
手眼标定的基本方程
设空间某点P在以上、、、的坐标为、、、,有如下关系:
(式4.1):
(式4.2):
(式4.3):
(式4.4):
(式4.1)+(式4.4)=(式4.5):
(式4.2)+(式4.3)=(式4.6):
(式4.5)+(式4.6)=(式4.7)手眼标定的基本方程:
式中:
- C:已知量,通过相机标定求得
- D:已知量,通过机器人控制器给出
- X:未知量,要求解的手眼关系矩阵
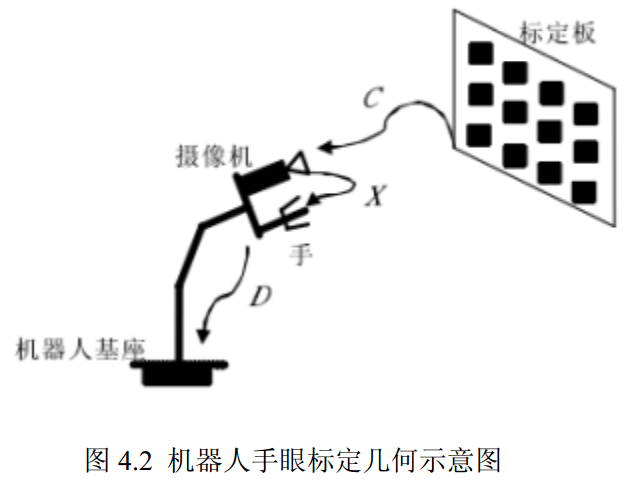
手眼标定模型的建立
在(式4.7)中,将C,D,X写成四阶方阵的形式,得(式4.8):
展开,得(式4.9)、(式4.10):
式中:
- 已知:、、、(、是正交单位矩阵)
- 求解:、(是正交单位矩阵)
Tsai手眼标定方法
(式4.9)、(式4.10)两个等式有无穷多解
矩阵R的3条性质:单位正交矩阵、旋转矩阵、矩阵分解
由(式4.10),得(式4.13):
手眼标定过程中,摄像机经过两个不同的位置(机器人做了两次运动),有关系式如下:
(式4.14):
(式4.15):
(式4.16):
(式4.17):
- 、、、:两次运动的旋转矩阵、平移向量,通过相机标定得到的外参数给出
- 、、、:通过读取机器人控制器上的姿态参数得到
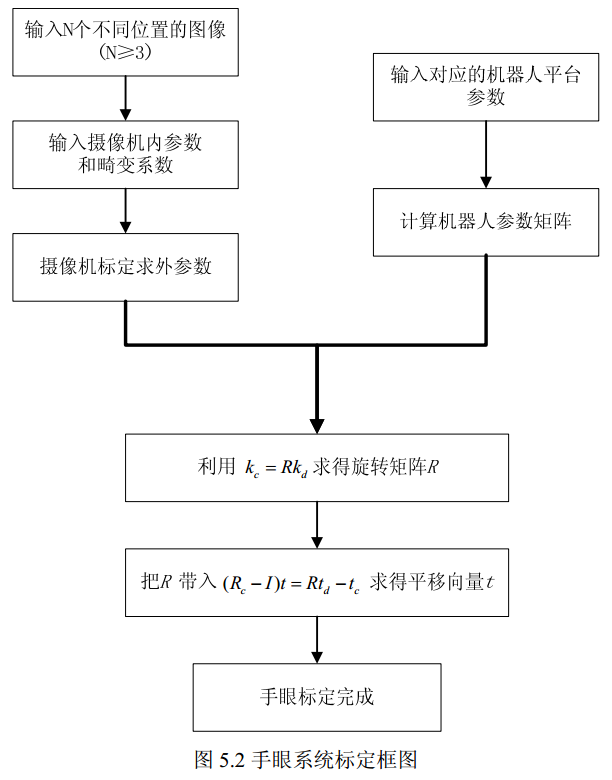
求解思路:
①(式4.14)、(式4.16) ⇒ R
②R、(式4.15)、(式4.17) ⇒ t
③手眼关系矩阵,标定完成
(式4.14)、(式4.16)的解R必须同时满足:
其中,、、、为、、、决定的旋转轴方向上的单位向量
得(式4.18):
当与不互相平行时,(式4.18)中的矩阵为满秩矩阵,有(式4.19):
把(式4.19)中解出的R代入(式4.15)、(式4.17),得到关于t的4个独立线性方程,而未知数是3个,可用最小二乘法从4个方程中解出t
直角坐标系中,机器人姿态由6个自由度(X Y Z TX TY TZ)确定
- (X Y Z):可确定姿态的平移向量
- (TX TY TZ):绕直角坐标系x,y,z轴的旋转角度,旋转矩阵
罗德里格斯变换:用、求其旋转轴、
标定软件系统的实现
软件架构
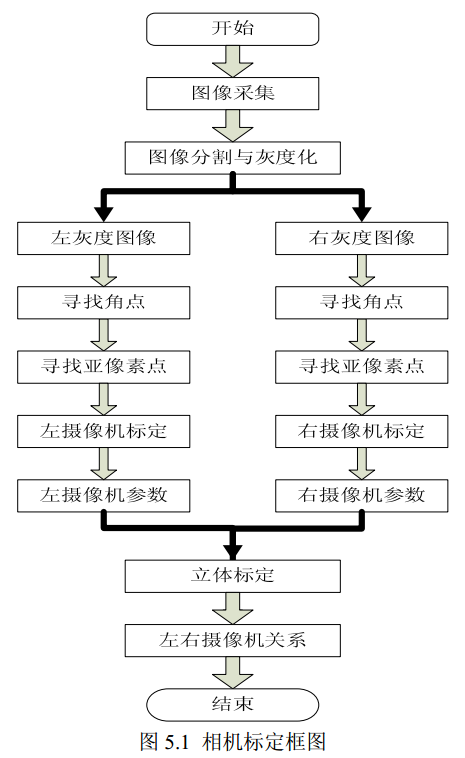
软件功能:立体标定、手眼标定
实现过程:
- 通过双目摄像机采集黑白棋盘格图像
- 通过OpenCV进行图像处理和相机标定 => 求得两个摄像机的内参数和外参数矩阵
- 进行立体标定 => 求得左右摄像机的位置关系
- 利用左摄像机的内参数、左摄像机拍摄的图像、对应的机器人姿态参数,进行手眼标定
机器人系统控制部分
串口RS232C、动态链接库
双目摄像机图像采集
MFC、动态链接库
OpenCV的API(图像处理、相机标定、立体标定、手眼标定)
| 模块 | 功能 | 函数(2.2的C++) | 3.4.1中的py函数 |
|---|---|---|---|
| 图像处理 | 转换为灰度图片 | cvCvtcolor() | cv2.cvtColor() |
| 图像处理 | 寻找角点 | cvFindChessboradCorners() | cv2.findChessboardCorners() |
| 图像处理 | 寻找亚像素点 | cvFindCornersSubPix() | cv2.cornerSubPix() |
| 图像处理 | 绘制找到的棋盘格角点 | cvDrawChessboardCorners() | cv2.drawChessboardCorners() |
| 相机标定 | 内参数 | cvCalibrateCamera2() | cv2.calibrateCamera() |
| 相机标定 | 外参数 | cvFindExtrinsicCalibrateCamera2() | cv2.calibrateCamera() |
| 立体标定 | 立体标定 | cvStereoCalibrate() | cv2.stereoCalibrate() |
| 手眼标定 | 标定函数 | cvFindExtrinsicCameraParams2() | cv2.solvePnP() |
| 手眼标定 | 罗德里格斯变换 | cvRodrigues2() | cv2.Rodrigues() |
标定结果分析
影响相机标定和手眼标定的主要因素:
- 机器人系统误差。系统误差,很难消除
- 图像的误差。光线很重要
- 摄像机光轴未能与末端执行器Z轴精确平行
- 标定板的精度。要求1.0μm