二维图形的5种几何变换
| 变换 | 英文 |
|---|---|
| 平移 | Translate |
| 旋转 | Rotate |
| 比例 | Scale |
| 反射 | Reflect |
| 错切 | shear |
平移
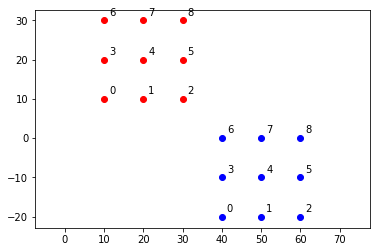
旋转
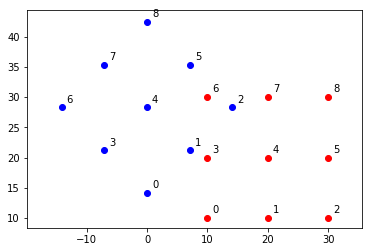
比例
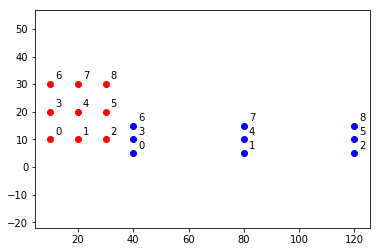
反射
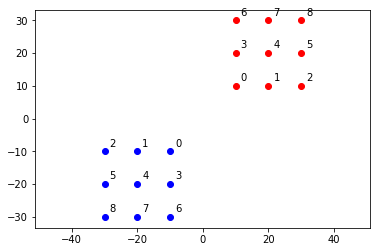
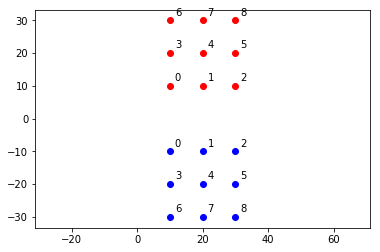
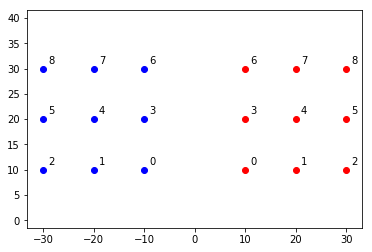
错切
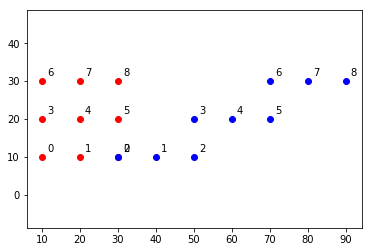
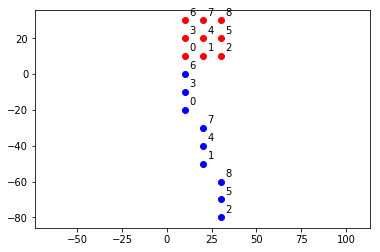
小结
符合下面形式的坐标变换称为二维仿射变换:
平移、旋转、比例、反射、错切都是二维仿射变换的特例,任何一组二维仿射变换总可表示为这5种变换的组合。
仿射变换具有平行线变换成平行线,有限点映射到有限点的一般特性。
VisionPro的CogCalibNPointToNPointTool的5种自由度
| 自由度 | 英文 | 含义 |
|---|---|---|
| 平移 | Translate | |
| 旋转 | Rotate | |
| 缩放 | Scale | |
| 纵横比 | Aspect | 缩放时xy比例不同 |
| 倾斜 | Skew | 旋转时xy角度不同 |
上述5种自由度均属于2D线性变换
CogCalibNPointToNPointTool功能:将图像坐标映射到“真实情况”坐标的二维转换,要求至少3个已知位置
2D线性变换(2D Linear Transformations)
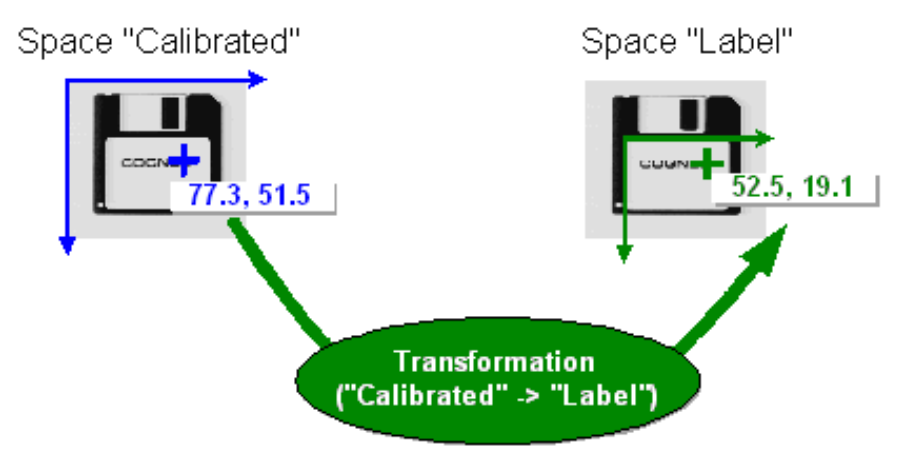
2D变换常用于将点从pixel space映射到user space,两者之间常常有不同的测量单位
包含3大类:
- 缩放(scaling)
- 旋转(rotation)
- 平移(translation)
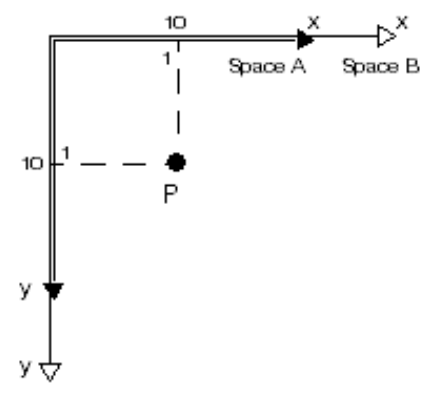
缩放(Scaling)
缩放:改变一个坐标空间相对于另一个坐标空间的x轴单位和y轴单位
均匀缩放(Uniform Scaling)
xy缩放比例相同
非均匀缩放(Nonuniform Scaling)
xy缩放比例不同,会改变坐标空间的纵横比(Aspect)
两种实现:
- 两个不同的缩放因子、
- 均匀缩放的缩放因子和附加的纵横比(Aspect)
旋转(Rotation)
旋转:相对于另一个坐标空间,旋转x和y轴(弧度)
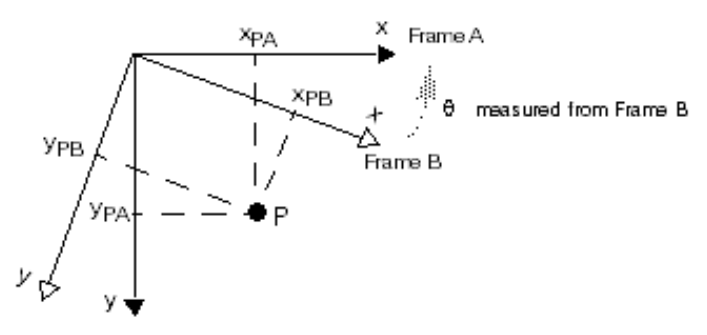
刚性旋转(Uniform or Rigid Rotation)
xy旋转角度相同
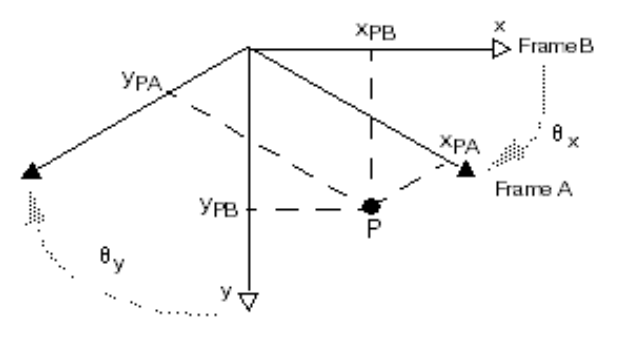
θ为点的逆时针方向旋转角
注意:旋转角度θ是在B中测量的,从空间B到空间A的角度
倾斜旋转(Nonuniform or Skew Rotation)
xy旋转角度不同
两种实现:
- 两个不同的旋转角度、
- 相同的旋转角度、附加的倾斜(Skew)因子
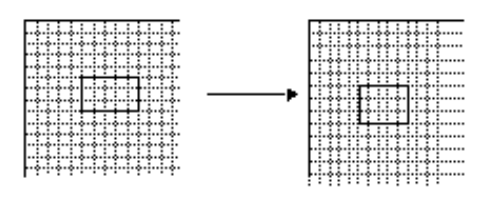
纵横比(Aspect)
纵横比:沿y轴的缩放因子与沿x轴缩放因子的比率
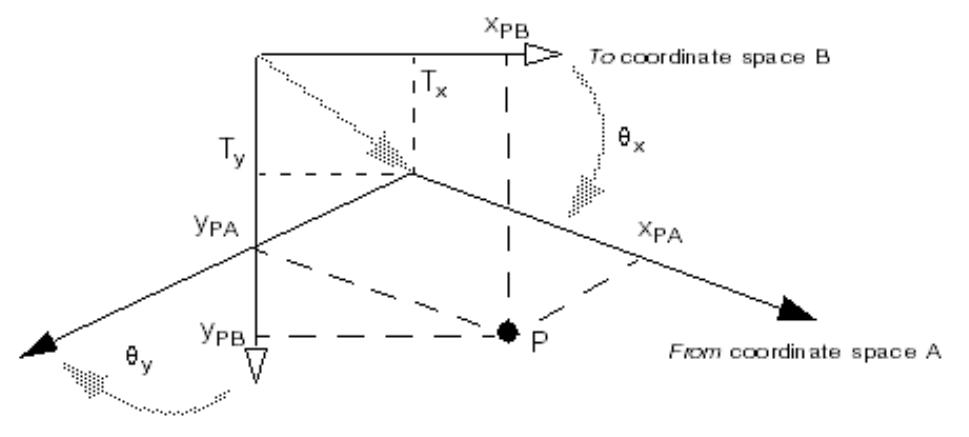
平移(Translation)
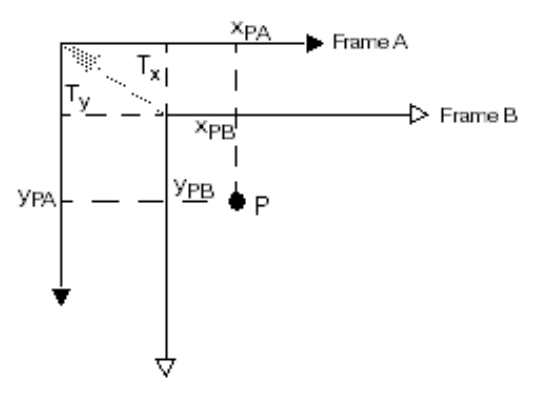
平移:由坐标空间相对于另一个坐标空间的原点的偏移量组成
如果是从坐标空间B到空间A的平移向量的分量,以空间B表示,则可以使用以下方法将空间A中的点P映射到空间B。
两种组合
两种组合只是视角不同,均为6个约束变量
ScalingX/Y-RotationX/Y Method
Scaling-Aspect-Rotation-Skew Method
VisionPro 2D Transformation Objects
方法:GetTransform()、MapPoint()
两步优化思路
| 符号 | 含义 | 维数 |
|---|---|---|
| N | 映射的点的个数 | N |
| w1 | 模板位的2D点坐标 | 3*N |
| w2 | 偏移位的2D点坐标 | 3*N |
| Rt | 通过伪逆求得的变换关系=w2*pinv(w1) | 3*3 |
| init | 由Rt求得的3个约束变量(旋转角度、x偏移、y偏移) | 3 |
| getRtFromRES() | 由约束变量求变换关系(3*3) | 3->3*3 |
| x0 | 第1次优化的结果 | 3 |
| x | 第2次优化的结果 | 3 |
| 优化步骤 | 优化量初始值 | 优化函数 | 目的 |
|---|---|---|---|
| 第1次优化 | init | getRtFromRES(init) - Rt | 得到满足物理约束的3个约束变量 |
| 第2次优化 | x0 | getRtFromRES(x0)*w1 - w2 | 使约束变量映射后的点与偏移位的点尽量接近 |
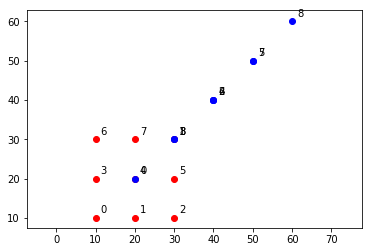
可视化
红点:模板(w1)
绿色:偏移(w2)
蓝色:估计(getRtFromRES(x)*w1)

参考
| 参考内容 | 参考方面 |
|---|---|
| 单目视觉标定:世界坐标系、相机坐标系、图像坐标系、像素坐标系——简单粗暴,粗暴 | 2D点到点的映射矩阵 |
| 使用 levenberg-marquardt 优化 欧式空间中的三维点变换关系 | 求点到点的映射的LM法优化思路 |
| 二维图形基本几何变换矩阵 | 二维图形的5种变化关系 |
| Cognex VisionPro Documentation 9.1中的Transformations | VisionPro的2D点变换 |