《A Flexible New Technique for Camera Calibration》

关键词：针孔模型、齐次形式

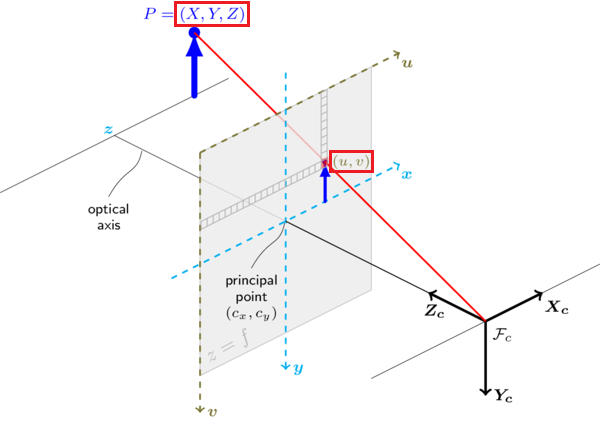
针孔相机模型（pinhole camera model）

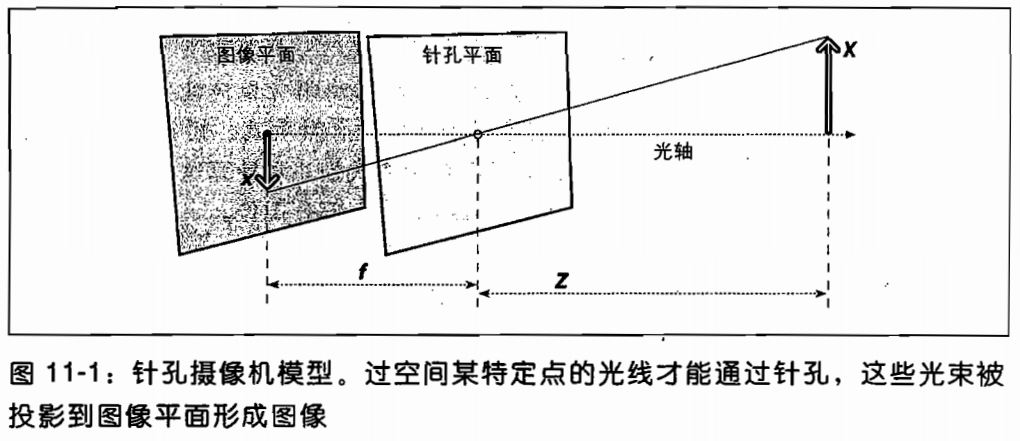
针孔模型：将相机简化成小孔成像，物理世界中的点“点”投影到成像表面

$- \frac{x}{f} = \frac{X}{Z}$

可将其整理成另一种等价形式：

$\frac{x}{f} = \frac{X}{Z}$

焦距 $f$ （ $OO_1$ ）：从针孔到图像平面的距离
其实上述焦距本质上是投影距离（是几何属性），不同于透镜的焦距（是透镜的属性）。对于透镜，当且仅当配置的焦距与镜头的焦距匹配时，图像才会对焦，故人们倾向于对这两个术语互换使用。
主点（ $O_1$ ）（principal point）：光轴与图像平面的交点
$p$ ：成像平面上一点，物理单位 $(x,y)$ ，像素单位 $(u,v)$ .
$P$ ：物理世界中一点，物理单位 $(X_c,Y_c,Z_c)$ .

$\frac{f}{Z_c} = \frac{x}{X_c} = \frac{y}{Y_c}$

公式推导

坐标系转换

像素图像坐标系 <=相机内参== 相机坐标系 <=相机外参== 世界坐标系

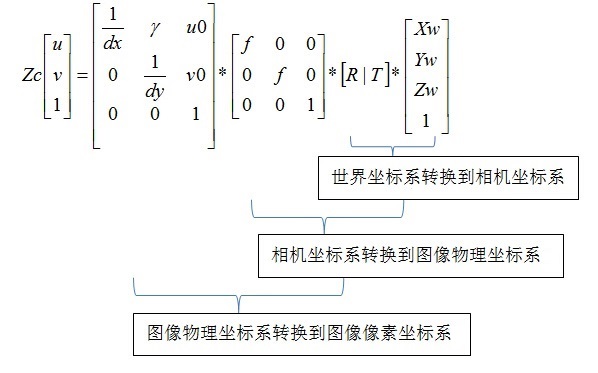
(1)像素图像坐标系 ↔ 物理图像坐标系

$u=\frac{x}{d_x}+u_0 \\ v=\frac{y}{d_y}+v_0 \\$

每像素的物理尺寸： $d_x,d_y$

整理成齐次坐标形式：
像素单位 ← 物理单位

$\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} \frac{1}{d_x} & 0 & u_0 \\ 0 & \frac{1}{d_y} & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} \tag{a}$

物理单位 ← 像素单位

$\begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} = \begin{bmatrix} d_x & 0 & -u_0d_x \\ 0 & d_y & -v_0d_y \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix}$

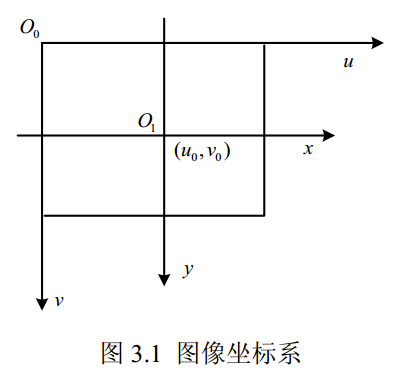
(2)图像坐标系 ↔ 相机坐标系

$\frac{f}{Z_c} = \frac{x}{X_c} = \frac{y}{Y_c}$

整理成齐次坐标形式：
物理图像坐标系 ← 相机坐标系：

$Z_c \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} = \begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \\ \end{bmatrix} \tag{b}$

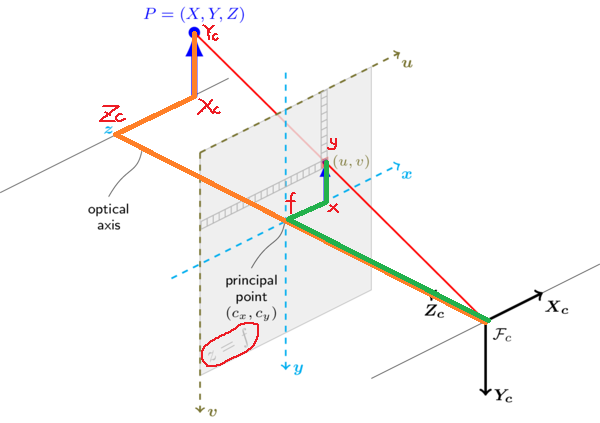
(3)相机坐标系 ↔ 世界坐标系

相机坐标系 ← 世界坐标系

$\begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 0 \\ \end{bmatrix} = \begin{bmatrix} R & t \\ 0^T & 1 \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{bmatrix} \tag{c}$

(4)像素图像坐标系 ↔ 世界坐标系

把 $式(a)$ 代入 $式(b)$ ：

$Z_c \begin{bmatrix} d_x & 0 & -u_0d_x \\ 0 & d_y & -v_0d_y \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \\ \end{bmatrix}$

左乘矩阵的逆 $inv(
\begin{bmatrix}
d_x & 0 & -u_0d_x \\
0 & d_y & -v_0d_y \\
0 & 0 & 1 \\
\end{bmatrix}
)=
\begin{bmatrix}
\frac{1}{d_x} & 0 & u_0 \\
0 & \frac{1}{d_y} & v_0 \\
0 & 0 & 1 \\
\end{bmatrix}
$：

$Z_c \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} \frac{1}{d_x} & 0 & u_0 \\ 0 & \frac{1}{d_y} & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \\ \end{bmatrix} \tag{d}$

把 $式(c)$ 代入 $式(d)$ ：
像素图像坐标系 ← 世界坐标系

整理可得：

$Z_c \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} \frac{f}{d_x} & 0 & u_0 & 0 \\ 0 & \frac{f}{d_y} & v_0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} R & t \\ 0^T & 1 \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{bmatrix}$ $Z_c \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} α_x & 0 & u_0 & 0 \\ 0 & α_y & v_0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{bmatrix}$

等式右边的前2个矩阵维度由 $(3*4 × 4*4)$ 变为 $(3*3 × 3*4)$ ，对结果无影响：
$
\begin{bmatrix}
α_x & 0 & u_0 & 0 \\
0 & α_y & v_0 & 0 \\
0 & 0 & 1 & 0 \\
\end{bmatrix}
\begin{bmatrix}
r_{11} & r_{12} & r_{13} & t_1 \\
r_{21} & r_{22} & r_{23} & t_2 \\
r_{31} & r_{32} & r_{33} & t_3 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\\
=
\begin{bmatrix}
α_x r_{11} + u_0 r_{31} & α_x r_{12} + u_0 r_{32} & α_x r_{13} + u_0 r_{33} & α_x t_1+ u_0 t_3 \\
α_y r_{21} + v_0 r_{31} & α_y r_{22} + v_0 r_{32} & α_y r_{23} + v_0 r_{33} & α_y t_2 + v_0 t_3 \\
r_{31} & r_{32} & r_{33} & t_3 \\
\end{bmatrix}
\\
=
\begin{bmatrix}
α_x & 0 & u_0 \\
0 & α_y & v_0 \\
0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
r_{11} & r_{12} & r_{13} & t_1 \\
r_{21} & r_{22} & r_{23} & t_2 \\
r_{31} & r_{32} & r_{33} & t_3 \\
\end{bmatrix}
$

故微调矩阵形式：

$Z_c \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} α_x & 0 & u_0 \\ 0 & α_y & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{bmatrix}$

而OpenCV文档中给出的公式如下，两者一致：

$s \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \\ \end{bmatrix}$

OpenCV中符号	我的公式中符号
$f_x=f · s_x\\f_y=f · s_y$	$α_x=\frac{f}{d_x}\\α_y=\frac{f}{d_y}$
$f_x$ ：以像素为单位的焦距（单位：像素） $f$ ：透镜的物理焦距长度（单位：毫米） $s_x$ ：成像装置每个单元尺寸（单位：像素/毫米）	$α_x=f_x$ $d_x$ ：每一个像素在x轴上的物理尺寸（单位：毫米/像素）
$s$	$Z_c$
$s$ ：比例因子	$Z_c$ ：物体在相机坐标系中的z坐标

OpenCV中的相关部分

针孔相机模型

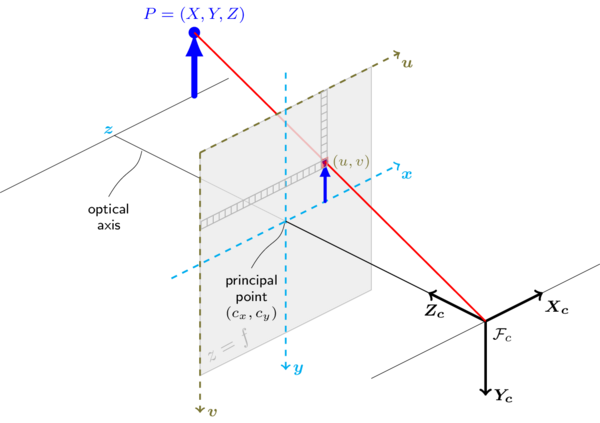
针孔相机模型：通过透视变换将3D点投影到图像平面中来形成场景视图

$s\ m' = A\ [R|t]\ M' \\ or \\ s \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \\ \end{bmatrix}$

$(X,Y,Z)$ ：世界坐标系的3D点
$(u,v)$ ：以像素为单位的投影点坐标（图像坐标系）
$A$ ：相机内参
$[R|t]$ ：相机外参
$(c_x,c_y)$ ：主点（通常在图像中心）
$f_x,f_y$ ：以像素为单位的焦距

上式等价于下式( $当z≠0$ )：

$\begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} = R \begin{bmatrix} X \\ Y \\ Z \\ \end{bmatrix} +t \\ x'=x/z \\ y'=y/z \\ u = f_x * x' +c_x \\ v = f_y * y' +c_y$

考虑畸变

$\begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} = R \begin{bmatrix} X \\ Y \\ Z \\ \end{bmatrix} +t \\ x'=x/z \\ y'=y/z \\ x''=x' \frac{1+k_1 r^2+k_2 r^4+k_3 r^6}{1+k_4 r^2+k_5 r^4+k_6 r^6} + 2 p_1 x' y' + p_2 (r^2 + 2 x'^2) + s_1 r^2 + s_2 r^4 \\ y''=y' \frac{1+k_1 r^2+k_2 r^4+k_3 r^6}{1+k_4 r^2+k_5 r^4+k_6 r^6}+ p_1 (r^2 + 2 y'^2) + 2 p_2 x' y' + s_3 r^2 + s_4 r^4 \\ where\ r^2 = x'^2 + y'^2 \\ u = f_x * x'' +c_x \\ v = f_y * y'' +c_y$

径向畸变（radial distortion）： $k_1,k_2,k_3,k_4,k_5,k_6$
切向畸变（tangential distortion）： $p_1,p_2$
薄透镜畸变（thin prism distortion）： $s_1,s_2,s_3,s_4$

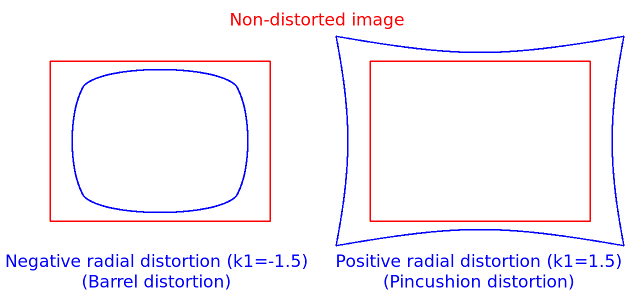
两种径向畸变：

桶型畸变（barrel distortion， $k_1<0$ ）
枕型畸变（pincushion distortion， $k_1>0$ ）

OpenCV还可以考虑图像传感器的倾斜，对于粒子图像测速（ particle image velocimetry，PIV）或使用激光扇的三角测量（triangulation with a laser fan）非常有用。
参数： $τ_x,τ_y$

所有的畸变系数（6+2+4+2=14个）：

$(k_1,k_2,p_1,p_2[,k_3[,k_4,k_5,k_6[,s_1,s_2,s_3,s_4[,τ_x,τ_y]]]])$

相机标定函数

1 2	retval, cameraMatrix, distCoeffs, rvecs, tvecs = cv2.calibrateCamera( objectPoints, imagePoints, imageSize, cameraMatrix, distCoeffs[, rvecs[, tvecs[, flags[, criteria]]]] )

标定的过程：

内参：$cameraMatrix=
\begin{bmatrix}
f_x & 0 & c_x \\
0 & f_y & c_y \\
0 & 0 & 1 \\
\end{bmatrix}$
- 相机的几何模型：相机的自然单位（像素）↔物理世界的单位（米）
- 透镜的畸变模型
外参：$rvecs, tvecs$

齐次坐标：便于在矩阵中表示平移

论文简述

总体步骤

估算单应性矩阵H
计算相机内参
计算径向畸变k1,k2,和相机外参
最大似然估计

基础方程

$s\ \widetilde{m} = A\ [R|t]\ \widetilde{M}$

实现功能

阅读源码

OpenCV

《学习OpenCV 3（中文版）》
相机模型——针孔相机
 内参、外参、畸变参数三种参数与相机的标定方法与相机坐标系的理解
 关于齐次坐标的理解（经典）
齐次坐标的理解
“齐次坐标表示是计算机图形学的重要手段之一，它既能够用来明确区分向量和点，同时也更易用于进行仿射（线性）几何变换。”
齐次坐标的理解