[机器视觉]双目视觉实验结果对比

发表于
将VisionPro中相机标定、手眼标定、姿态偏移的结果，与OpenCV、Matlab做对比。

一个想法：立体标定后再三角定位、点的归一化、基于SVD的三角测量

实验思路

实验设计

实验 相机标定 手眼标定
实验1 VisionPro VisionPro
实验2 OpenCV OpenCV
实验3 OpenCV VisionPro
实验4 VisionPro OpenCV

对照组

目的 对照组
比较OpenCV与VisionPro的总体性能 实验1、实验2
验证相机标定对总体性能的影响（如果三者结果类似，说明相机标定对总体性能影响小） ①实验1、实验3
②实验2、实验4
验证手眼标定对总体性能的影响（如果三者结果类似，说明手眼标定对总体性能影响小） ①实验1、实验4
②实验2、实验3

相机标定

Matlab

使用Camera Calibrator APP

值得注意的功能

  1. 指定估计的模型
    • 径向畸变（Radial Distortion）：2个系数/3个系数
    • 斜交（Skew）：是否考虑
    • 切向畸变（Tangential Distortion）：是否考虑
  2. 衡量标定效果
    • 重投影误差（Reprojection Errors）画图，可过滤掉重投影误差大的
    • 可视化的方式观察外参：固定相机/移动相机
    • 显示无畸变的图像
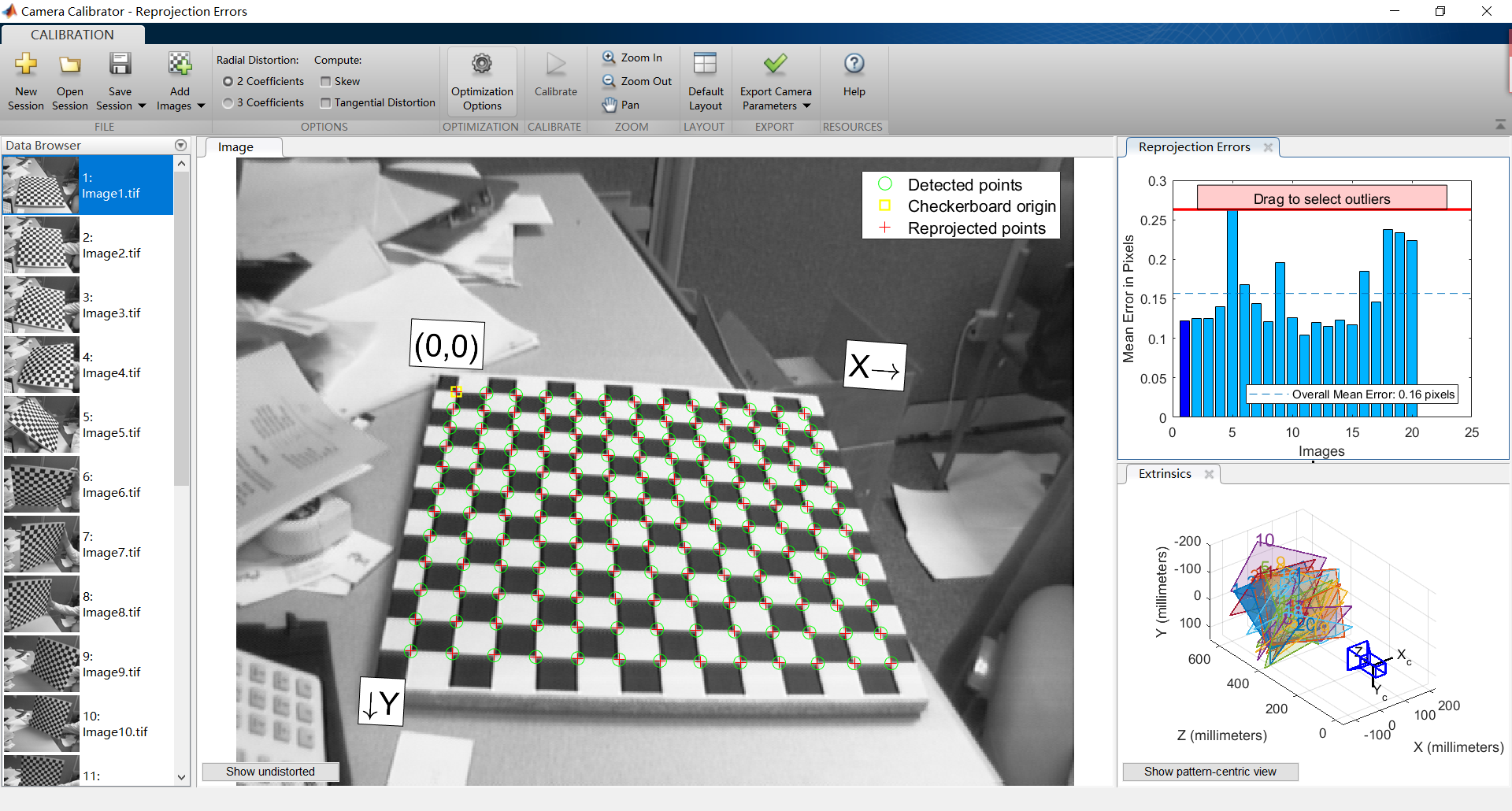
  3. Matlab的误差计算方式是欧氏距离：MeanReprojectionError — Average Euclidean distance
  4. Matlab提供了计算世界坐标的函数：cameraParameters类中有方法pointsToWorld、worldToImage
    • pointsToWorld()：
    • worldToImage()：

与OpenCV对应关系

Matlab与OpenCV中的相机标定完全一致
Matlab中2D角点必须对齐后才能输入函数，OpenCV则没有此限制
表示方式上，两者的内参互为转置

相机标定

Matlab代码：

1
2
3
4
5
6
7
8
9
% size(imagePoints) = (170, 2, 9)
% size(worldPoints) = (170, 2)
% [mrows, ncols] = [2050, 2448]
% 故在Matlab中2D角点必须对齐后才能输入函数，因为worldPoints比imagePoints少一个维度
[cameraParams, imagesUsed, estimationErrors] = estimateCameraParameters(imagePoints, worldPoints, ...
    'EstimateSkew', flag_skew, 'EstimateTangentialDistortion', flag_tangential, ...      % false/true, false/true
    'NumRadialDistortionCoefficients', num_radial, 'WorldUnits', 'millimeters', ...      % 2/3
    'InitialIntrinsicMatrix', [], 'InitialRadialDistortion', [], ...
    'ImageSize', [mrows, ncols]);

OpenCV代码：

1
2
3
4
# len(obj_list) == len(img_list) == 9
# obj_list[0].shape == (170, 3)
# img_list[0].shape == (170, 2)
ret, mtx33_cameraIntrinsic, dist, rvecs, tvecs = cv2.calibrateCamera(obj_list, img_list, (2448, 2050), None, None, flags=0)

径向畸变 Skew 切向畸变 calibrateCamera()的flags
2系数 不考虑 不考虑 cv2.CALIB_ZERO_TANGENT_DIST+cv2.CALIB_FIX_K3
3系数 不考虑 不考虑 cv2.CALIB_ZERO_TANGENT_DIST
2系数 不考虑 考虑 cv2.CALIB_FIX_K3
3系数 不考虑 考虑 0

相机内外参

比较条目 Matlab OpenCV
相机内参 cameraParams.IntrinsicMatrix’ mtx33_cameraIntrinsic
径向畸变 cameraParams.RadialDistortion dist.flatten()[[0,1,4]]
切向畸变 cameraParams.TangentialDistortion dist.flatten()[[2,3]]
相机外参 cameraParams.RotationMatrices(:,:,1)’
cameraParams.TranslationVectors(1,:)		 cv2.Rodrigues(rvecs[0])[0]
tvecs[0]

对点纠正畸变

Matlab代码：

1
2
% 对第1个姿态的第1个点纠正畸变
undistortPoints(imagePoints(1,:,1), cameraParams)

OpenCV代码：

1
2
3
4
# 先纠正畸变,再化为齐次形式,再左乘内参
point_undistorted = cv2.undistortPoints(img_list[0][0].reshape(1,1,2), mtx33_cameraIntrinsic, dist)
point_undistorted = np.array(point_undistorted.flatten().tolist() + [1]).reshape(3,1)
pointCam2D_undistorted = np.dot(mtx33_cameraIntrinsic, point_undistorted).flatten()[0:2]

已知内参求外参

Matlab代码：

1
2
3
4
5
6
7
8
9
% 对第idx个姿态求外参
idx = 1;
imagePoints_undistorted = undistortPoints(imagePoints(:,:,idx), cameraParams);
[R,t] = extrinsics(imagePoints_undistorted, worldPoints, cameraParams);

% R、t是extrinsics()求得的
% R0、t0是estimateCameraParameters()求得的，两者几乎完全等同
R0 = cameraParams.RotationMatrices(:,:,idx);
t0 = cameraParams.TranslationVectors(idx,:);

OpenCV代码：

1
2
3
4
5
idx = 0
retval_, rvec_, tvec_ = cv2.solvePnP(obj_list[idx], img_list[idx], mtx33_cameraIntrinsic, dist)

# rvec_、tvec_是cv2.solvePnP()求得的
# rvecs[idx]、tvecs[idx]是cv2.calibrateCamera()求得的，两者完全等同

OpenCV

OpenCV源码的Python例程中与标定相关的：calibrate.py、camera_calibration_show_extrinsics.py、test_calibration.py

flag参数

calibrateCamera()函数的flag参数：

flag值 含义
0 默认值
cv2.CALIB_USE_INTRINSIC_GUESS 指定算法初始化的相机内参（fx, fy, cx, cy）
不指定会报错
cv2.CALIB_FIX_PRINCIPAL_POINT 在全局优化中，主点不改变
即按默认cx, cy为图像大小的一半
cv2.CALIB_FIX_ASPECT_RATIO 仅将fy视为自由参数
cv2.CALIB_ZERO_TANGENT_DIST 忽略切向畸变，即p1, p2设置为0且一直为0
cv2.CALIB_FIX_K1 … cv2.CALIB_FIX_K6 在优化过程中保持k1/…/k6不变，默认是0
cv2.CALIB_RATIONAL_MODEL k4、k5、k6被启用，返回的distCoeffs由5个值变为8个值
cv2.CALIB_THIN_PRISM_MODEL s1、s2、s3、s4被启用，返回的distCoeffs由5个值变为8个值
cv2.CALIB_FIX_S1_S2_S3_S4 优化期间，薄透镜系数不改变
cv2.CALIB_TILTED_MODEL 系数τx、τy被启用，返回的distCoeffs由5个值变为7个值
cv2.CALIB_FIX_TAUX_TAUY 优化期间，倾斜传感器模型的系数不改变

迭代求解系数

OpenCV迭代求解的所有系数：(fx,fy,cx,cy,k1,k2,p1,p2,k3,k4,k5,k6,s1,s2,s3,s4,τx,τy)

  • 内参：(fx,fy,cx,cy) —— 4个
  • 畸变系数：(k1,k2,p1,p2[,k3[,k4,k5,k6[,s1,s2,s3,s4[,τx,τy]]]]) —— 14个
    • 径向畸变：k1~k6
    • 切向畸变：p1、p2
    • 薄透镜畸变：s1~s4
    • 倾斜传感器：τx、τy

VisionPro

1
2
3
4
5
6
7
Cog3DCameraCalibrationResult = Cog3DCameraCalibrator.Execute
(
	List<Rectangle>, ——图像大小（如2448×2050）
	List<List<Cog3DCrspFeaturesCollection>>, ——特征点对（Raw2D、Phys3D）
	Cog3DScalarCollection, ——高度（如0）
	List<Cog3DCalibrationPlatePoseTypeConstants> ——姿态类型（如倾斜）
)

总体的衡量指标：

指标 内容 举例
MaximumTilt 所有测量姿态的棋盘格最大倾斜 0.27318
NumCalPlatePoses 棋盘格姿态数量 9
NumCameras 相机数量 2
☆OverallResidualsRaw2D Raw2D中的总体残差统计数据（在所有相机和所有标定板姿势上） < Cog3DResiduals : Max 8.816 Rms 1.068 >
☆OverallResidualsPhys3D Phys3D中的总体残差统计数据（在所有相机和所有标定板姿势上） < Cog3DResiduals : Max 1.564 Rms 0.166 >

Cog3DCameraCalibrationResult.OverallResidualsPhys3D：Residual error in Phys3D space is the distance between a ray of any 2D feature (generated using the estimated camera calibration data) and its corresponding 3D feature.

Cog3DCameraCalibrationResult.OverallResidualsRaw2D：Residual error in Raw2D space is the distance from the found location of any 2D feature in the image to the 2D location that you would expect if you took the 3D feature and mapped it using the estimated camera calibration data.

Cog3DHandEyeCalibrationResult.PositionResidualsPhys3D：Gets the overall residual statistics. These statistics represent all mapped samples from all stations.

Remarks

每个相机每个姿态的衡量指标：

指标 内容 举例
FeatureCoverageOfCamera
（1个）		 在所有标定板姿态中的特征点对的凸包覆盖的特定相机视野的比例 0.85801
NumCorrespondences
（9个）		 在特定标定板姿态、特定相机的对应关系数 222
FeatureCoverageOfCameraPlate
（9个）		 在特定标定板姿态中的特征点对的凸包覆盖的特定相机视野的比例 0.80139
CalPlate3DFromCamera3D
（9个）		 Camera3D->CalPlate3D
相机外参		 Cog3DTransformRigid（4×4）
Camera3DFromPhys3D Phys3D->Camera3D
相机外参
ResidualsRaw2D
（9个）		 Raw2D中的残差统计数据（在特定相机和特定标定板姿势上） < Cog3DResiduals : Max 5.238 Rms 1.028 >
ResidualsPhys3D Phys3D中的残差统计数据（在特定相机和特定标定板姿势上）
GetPhys3DFromCalPlate3Ds() CalPlate3D->Phys3D
每个姿态相对于第1个姿态（世界坐标系）的变换
GetRaw2DFromCamera2Ds() Camera2D->Raw2D
相机内参
GetRaw2DFromPhys3Ds() Phys3D->Raw2D
标定的所有结果

手眼标定

姿态偏移

参考

参考内容 参考方面
MATLAB “Camera Calibrator APP”的使用 matlab自带相机标定工具箱的使用
OpenCV中的相机标定函数 算法的输入输出、总体流程
MATLAB相机标定工具箱 标定流程、可视化工具（没用到）
《A flexible new technique for camera calibration》 张正友的相机标定论文
内参、外参、畸变参数三种参数与相机的标定方法与相机坐标系的理解
OpenCV仿射变换+投射变换+单应性矩阵
HALCON文档
HALCON Operator Reference HALCON算子手册
HALCON中的相机标定算子、手眼标定算子

HALCON文档中出现的参考文献（References）

Chapter 6 Calibration

6.4 Hand-Eye P368
K. Daniilidis: “Hand-Eye Calibration Using Dual Quaternions”; International Journal of Robotics Research, Vol. 18, No. 3, pp. 286-298; 1999.
M. Ulrich, C. Steger: “Hand-Eye Calibration of SCARA Robots Using Dual Quaternions”; Pattern Recognition and Image Analysis, Vol. 26, No. 1, pp. 231-239; January 2016.

6.7 Multi-View P394
Carsten Steger: “A Comprehensive and Versatile Camera Model for Cameras with Tilt Lenses”; International Journal of Computer Vision, vol. 123, no. 2, pp. 121-159, 2017.

6.10 Self-Calibration P443
T. Thormälen, H. Broszio: “Automatic line-based estimation of radial lens distortion”; in: Integrated Computer Aided Engineering; vol. 12; pp. 177-190; 2005.
P451
Lourdes Agapito, E. Hayman, I. Reid: “Self-Calibration of Rotating and Zooming Cameras”; International Journal of Computer Vision; vol. 45, no. 2; pp. 107–127; 2001

Chapter 27 Transformations

27.5 Poses P2569
[1] Francesc Moreno-Noguer, Vincent Lepetit, and Pascal Fua: “Accurate Non-Iterative O(n) Solution to the PnP Problem”; Eleventh IEEE International Conference on Computer Vision, 2007.
[2] Gerald Schweighofer, and Axel Pinz: “Robust Pose Estimation from a Planar Target”; Transactions on Pattern Analysis and Machine Intelligence (PAMI), 28(12):2024-2030, 2006.
[3] Carsten Steger: “Algorithms for the Orthographic-n-Point Problem”; Journal of Mathematical Imaging and Vision, vol. 60, no. 2, pp. 246-266, 2018.
[4] Zhengyou Zhang: “A flexible new technique for camera calibration.”; Transactions on Pattern Analysis and Machine Intelligence (PAMI), 22(11):1330-1334, 2000